Recursion

Chapter Goals

• To learn about the method of recursion
• To understand the relationship between recursion and iteration
• To analysis problems that are much easier to solve by recursion than by iteration
• To learn to think recursively
• To be able to use recursive helper methods
• To understand when the use of recursion affects the efficiency of an algorithm

Triangle Numbers

• Compute the area of a triangle of width n
• Assume each [] square has an area of 1
• Also called the nth triangle number
• The third triangle number is 6

[]
[] []
[] [] []

Outline of Triangle Class

public class Triangle
{
    public Triangle(int aWidth)
    {
       width = aWidth;
    }
    public int getArea()
    {
       ...
    }
    private int width;
} 

Handling Triangle of Width 1

• The triangle consists of a single square
• Its area is 1
• Add the code to getArea method for width 1

public int getArea()
{
    if (width == 1) return 1;
}

Handling General Case

[]
[] []
[] [] []
[] [] [] []

• Assume we know the area of the smaller, colored triangle
• Area of larger triangle can be calculated as
             smallerArea + width
• To get the area of the smaller triangle
  -make a smaller triangle and ask it for its area
  

  Triangle smallerTriangle = new Triangle(width - 1);
  int smallerArea = smallerTriangle.getArea();
  

• Completed getArea method
  

  public int getArea()
  {
      if (width == 1) return 1;
      Triangle smallerTriangle = new Triangle(width - 1);
      int smallerArea = smallerTriangle.getArea();
      return smallerArea + width;
  }
  

Computing the area of a triangle with width 4

• getArea method makes a smaller triangle of width 3
• It calls getArea on that triangle
• That method makes a smaller triangle of width 2
• It calls getArea on that triangle
• That method makes a smaller triangle of width 1
• It calls getArea on that triangle
• That method returns 1
• The method returns smallerArea + width = 1 + 2 = 3
• The method returns smallerArea + width = 3 + 3 = 6
• The method returns smallerArea + width = 6 + 4 = 10

Recursion

• A recursive computation solves a problem by using the solution of the same problem with simpler input.
• For recursion to terminate, there must be special cases for the simplest inputs.
  - To complete our Triangle example, we must handle width <= 0
  - add this line to the getArea method
               if (width <= 0)  return 0;

File Triangle.java

TriangleTest.java

Permutations of a String

• Design a class that will list all permutations of a string
• A permutation is a rearrangement of the letters
• The string "eat" has six permutations
  

  "eat"
  "eta"
  "aet"
  "tea"
  "tae"
  

Public Interface of PermutationGenerator

class PermutationGenerator
{
    public PermutationGenerator(String s) { . . . }
    public String nextPermutation() {. . . }
    public boolean hasMorePermutations() { . . . }
}

File PermutationGeneratorTest.java

To Generate All Permutations

• Generate all permutations that start with 'e' , then 'a' then 't'
• To generate permutations starting with 'e', we need to find all permutations of "at"
• This is the same problem with simpler inputs.
• Use recursion
• nextPermutaion method returns one permutation at a time
• PermutationGenerator remembers it state
  - the string we are permuting (word)
  - position of the current character (current)
  - a PermutationGenerator of the substring (tailGenerator)
• nextPermutation asks tailGenerator for its next permutation and returns
        word.charAt(current) + tailGenerator.nextPermutation();

Handling the Special Case

• Increment the current position
• Compute the tail string that contains all letters except for the current one
• Make a new permutation generator for the tail string

File PermutationGenerator.java

Recursive Helper Method

• The public boolean method isPalindrone( ) calls helper method
  isPalindrome(int start, int end)
• Helper method skips over matching letter pairs and non-letters and calls itself recursively

public boolean isPalindrome(int start int end)
{
   //separate case for substrings of length 0 or 1
   if (start>=end) return true;

   //get first and last character, converted to lowercase
   char first = Character.toLowerCase(text.charAt(start));
   char last = Character.toLowerCase(text.charAt(end));

   if ((Character.isLetter(first) && Character.isLetter(last))
   {
      if (first == last)
      {
         //test substring that doesn't contain the matching letters
         return isPalindrome(start +1, end -1);
      }
      else
         return false;
   }
   else if (!Character.isLetter(last))
   {
      //test substring that doesn't contain last character
      return isPalindrome(start, end -1);
   }
   else
   {
      //test substring that doesn't contain first character
      return isPalindrome(start + 1, end);
}
   

Using Mutual Recursion

Problem: to compute the value of arithmetic expressions such as

3 + 4 * 5
(3 + 4) * 5
1 - (2 - (3 - (4 - 5)))

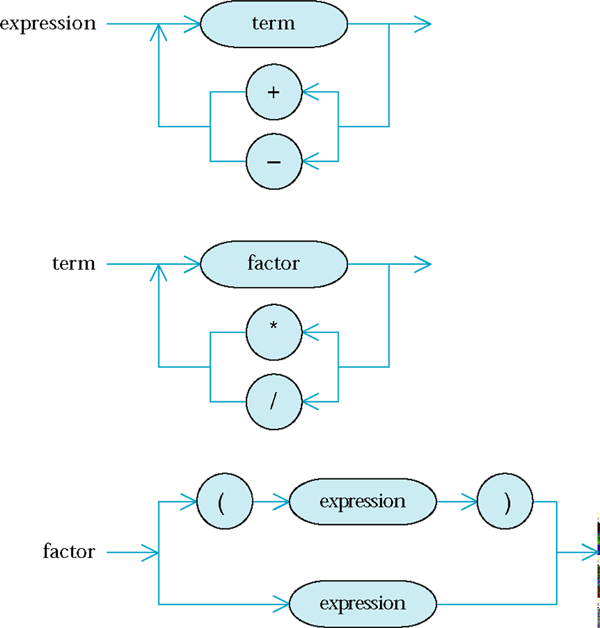
Syntax Diagram for Evaluating and Expression

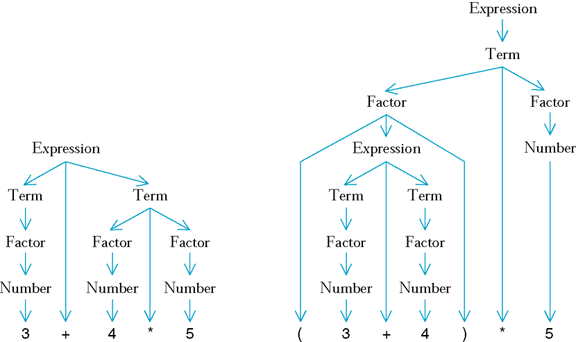
Syntax Tree for Two Expressions

Mutually Recursive Methods

• Implement 3 methods that call each other recursively
  • getExpressionValue
  • getTermValue
  • getFactorValue

File Evaluator.java

File ExpressionTokenizer.java

File EvaluatorTest.java

Fibonacci Sequence

• Fibonacci sequence is a sequence of numbers defined by
  

  f₁  =  1
  f₂  =   1
  f_n  =  f_n-1  +  f_n-2

• First ten terms

  1, 1, 2, 3, 5, 8, 13, 21, 34, 55

The Efficiency of Recursion

• You can generate the Fibonacci series using either recursion or iteration
  • Both are conceptually easy to understand and program
  • Iterative solution is much faster
• Palindrome test can be implemented as either recursion or iteration
  • Both are easy to program
  • Both run about the same speed
• Permutation generator can be solved using either recursion or iteration
  • Recursive solution is dramatically easier to understand and implement
  • Both run at about the same speed

File FibTest.java

Call Pattern of the Recursive fib Method

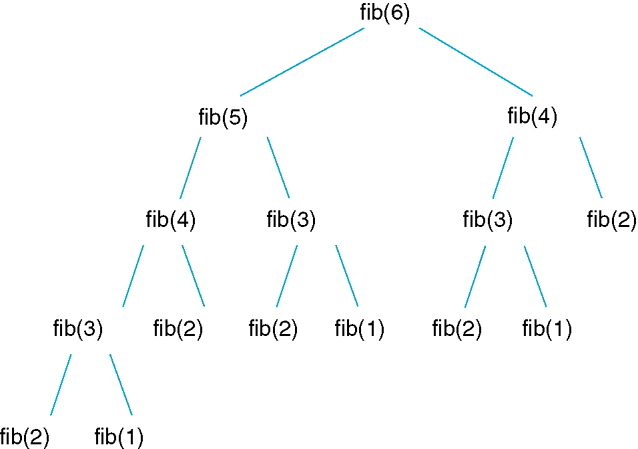
File FibTrace.java

File FibLoop.java